La
force de Coriolis
Impossible d'ouvrir
un ouvrage de météorologie sans rencontrer la notion de (pseudo-)force
de Coriolis (voir note1). Et donc pour un marin,
impossible de comprendre sans elle
la raison physique de l'orientation du
vent dans une
dépression (loi de Buys-Ballot http://fr.wikipedia.org/wiki/Loi_de_Buys-Ballot)
ou de prévoir la force du vent en
fonction du champ de pression (vent géostrophique http://fr.wikipedia.org/wiki/Vent_g%C3%A9ostrophique)
Or
il est impossible (à ma connaissance) de donner une
présentation
purement intuitive de cette force. Ce n'est pas un hasard s'il a fallu
attendre les
travaux de Coriolis en 1835 pour une première présentation, date bien
tardive pour la mécanique classique déjà bien constituée au cours du
XVIIIe
siècle (cf.
http://fr.wikipedia.org/wiki/Force_de_Coriolis. Et ce n'est qu'à la
fin du XIXe siècle que cette
force fit son apparition dans la littérature météorologique et
océanographique. On peut lire à ce propos le travail d'A.
Persson, The Coriolis Effect – a
conflict between common sense and mathematics : http://retro.met.no/english/topics/nomek_2005/coriolis.pdf
signalé dans l'article anglais de Wikipédia Coriolis effect.).
Il faut donc une présentation physico-mathématique soignée, ce que
cette
page tente de faire, avec une attention particulière aux 'rappels'
préalables (pour une présentation de la notion de vecteur, voir
notre
page ../NavigationAstro/vecteur.html
)
Mais heureusement, dès que les notions d'accélération dans le mouvement
circulaire et
de force centripète / centrifuge sont maîtrisées, on peut donner une
présentation correcte de la force de Coriolis dans le cas particulier
important d'un mouvement sur la terre dans la direction ouest - est
(voir §2). Et après avoir maîtrisé les notions de moment angulaire et
cinétique, il est possible de saisir l'orientation de la force de
Coriolis dans un déplacement sur un axe nord-sud (voir §5).
0
- Le produit
vectoriel
0.1
Définitions et propriétés
La notion de produit vectoriel
est un outil (presque)
indispensable
pour manipuler
facilement des données
physiques vectorielles (c'est
à dire non-scalaires) dans un espace
à deux ou trois
dimensions.
Le produit vectoriel n'est pas une découverte ou un théorème, mais
juste une manière
astucieuse et compacte de représenter des vecteurs dans un espace à
plusieurs
dimensions.
Par
définition, le résultat du produit
vectoriel des deux vecteurs OA
et OB
(donc de même origine O), noté
OA
x OB
(et quelquefois
OA Λ OB) est un autre vecteur.
Ce nouveau vecteur (dont on peut placer l'origine
également en O) est tel que
OA x OB = OA OB sin α u
où
- α est l'angle entre les deux vecteurs,
compté de OA vers OB, et
- u
est le vecteur
unité perpendiculaire
au plan AOB.
• Il est tout d'abord facile de vérifier que le
module OA
OB sin α de ce nouveau vecteur est l'aire du parallélogramme construit
sur OA et OB (fig. 0.1).
En
effet, les
triangles OBB" et AB'A' sont égaux, et l'aire du parallélogramme OBB'A
est la
même que celle du rectangle BB'A'B", qui a
pour aire OA OB sin α (Fig. 0.1)
•
Le sens de u
obéit
à la convention (ou règle arbitraire) suivante: imaginons OA
comme le manche d'un clé et u
comme une tige fileté: u
est dans le sens positif lorsqu'en tournant le manche de OA vers OB, on
"vise un écrou" sur u (fig.
0.2)



Fig.
0.1
Fig.
0.2
Fig. 0.3
• Une
propriété essentielle
du produit vectoriel est
A
x A = 0
car
comme sin(0) = 0, A A sin (0) = 0
Plus
généralement, le produit
vectoriel de deux vecteurs parallèles
est nul: quels que soient les modules, on a
sin(0) =0
• Une seconde propriété est que le
produit vectoriel est antisymmétrique:
en effet, A
x B = - B x A
car
sin α
= - sin(α)
0.2
Sens
négatif ou positif des produits vectoriels des vecteurs unités de
l'espace
Considérons la fig. 0.3 qui présente les 3 vecteurs unités de
l'espace. En suivant les règles et propriétés énoncés ci-dessus, on a
i x j = k
d'où j
x i = - k (par antisymmétrie). De
même
i
x k = - j
k x i = j
j x k =
i
k x j = - i
et
i
x i, j x j,
k x k = 0
(car un vecteur est parallèle à lui-même)
On peut facilement retrouver ces relations par le
moyen graphique suivant (fig. 0.4)
Sur un
cercle orienté positivement dans le sens inverse du sens de
rotation des aiguilles
d'une
montre, placer i,
j, k le long du cercle
dans le sens
positif.
Le sens du vecteur
unité
résultat est positif quand on tourne dans le sens
positif. Par exemple, j x k donnera
i car on tourne
dans le sens positif;
i x k donnera
-j car en
allant de
i à k pour
aboutir à j,
on tourne dans le sens négatif;

Fig. 0.4
0.3 Expression
du produit
vectoriel en fonction des
composantes des vecteurs
Soit le vecteur
A
= ax
i + ay
j
+ az k
et
B
= bx
i + by
j
+ bz k
A
x B
= (ax
i + ay
j
+ az k) x (bx
i + by
j
+ bz k)
= ax
i bx
i
= 0
+ ax
i by
j
= ax by
k
+ ax
i bz
k
= -
ax bz
j
+ ay
j bx
i
= - ay bx k
+ ay
j by
j
= 0
+
ay j
bz k
= ay bz
i
+ az
k bx
i
= az
bx
j
+ az
k by
j
= - az by
i
+ az
k bz
k
= 0
d'où
A
x B
= (ay bz
- az by) i + (az bx - ax bz) j + (ax by -
ay bx) k
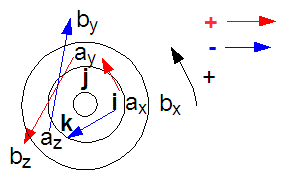
Fig. 0.5
Pour retrouver les
produits de composantes: placez i,
j, k avec leurs
composantes correspondantes dans le sens positif sur trois cercles
concentriques (cf. Fig. 0.5)
Pour
trouver les produits positifs, tournez à partir d'un vecteur unité dans
le sens positif de l'intérieur et vers l'extérieur.
Pour trouver
les
produits négatifs, tournez dans le sens négatif de l'intérieur vers
l'extérieur (On peut aussi simplement échanger le nom des
composantes)
Par
exemple : i
: + ay bz , i
: - az by
(ou échangez les noms des composantes : ay donne
by
, bz donne az)
Le produit vectoriel se met quelquefois sous la forme d'un 'déterminant
symbolique'
|
i
j
k
|
| ax
ay
az
|
| bx
by
bz
|
Les composantes se calculent 'en croix' de manière cyclique...
j
k
|
i
j
k
| i
j
ay
az
| ax
ay
az |
ax
ay
by bz | bx
by
bz | bx
by
De i
sur la première ligne, descendre à droite
vers ay puis bz, qui sont
affectés du signe positif
De i sur
la première ligne, descend à gauche vers - az
puis - by, qui sont
affectés du signe négatif
....
d'où
A
x B
= (ay bz
- az by) i + (az bx - ax bz) j + ( ax by -
ay bx) k
1 - Vitesse et accélération
sous la forme d'un produit vectoriel dans le mouvement circulaire
uniforme
1.1 Vitesse, accélération et
forces centripète et centrifuge
Depuis Newton, on sait qu'en l'absence de force le mouvement d'un
corps dans l'espace est rectiligne à vitesse constante (avec,
comme cas particulier, l'immobilité ou repos du corps quand la vitesse
est nulle).
Tout changement de vitesse et /
ou de direction exige donc l'intervention d'une force.
La force
F, la masse m
du corps et l'accélération γ
qui en résulte sont liés par la relation
vectorielle fondamentale qui définit F.
F
= m γ
(Dans
le cas d'une masse unité, on a évidemment F
= γ)
Un
objet tournant le long d'un cercle est dit animé d'un mouvement
circulaire uniforme
si le module
v = |V| de son
vecteur vitesse V
est constant.
En revanche, comme la direction
de V
change
continûment, il y a donc nécessairement accélération. En effet, les vecteurs
vitesse V
et V' au
temps t et t' ne sont pas
équipollents (même direction, sens et module). Le mouvement
n'est donc PAS rectiligne à
vitesse constante.
Un mouvement circulaire uniforme suppose donc
une
accélération, le vecteur vitesse V
changeant en effet constamment de direction. Et il y a donc
obligatoirement l'intervention
d'une
force.
La force qui s'applique à un objet dans le mouvement circulaire
est appelée force
centripète (Fig. 1.1) C'est la force qu'on doit appliquer à un
objet fixé au bout d'une cordelette pour le faire tournoyer.


Fig. 1.1
Fig.
1.2
Nous verrons que la force centripète est dirigée vers le centre du
cercle. Sans entrer maintenant dans le détail de son calcul, regardons
la figure 1.2. Au temps t, supposons que l'objet qui se déplace le long
d'un
cercle est au point A. Au temps t', il est en A'. V et V' sont
les vecteurs vitesse à ces deux instants. Pour calculer le vecteur
différence V' - V (qui
correspond dans le cas d'un intervalle de temps Δt très petit au ΔV de
l'accélération ΔV /Δt), il faut évidemment donner une origine commune
aux deux vecteurs. Ce vecteur différence, lié à la force centripète,
est en rouge sur la figure 1.2: il est visiblement tourné vers
l'intérieur du cercle.
Mais supposons maintenant que je sois assis sur le siège d'un manège en
rotation à vitesse constante. Pour
me faire décrire un cercle, le siège doit exercer sur moi une force centripète, sinon je
poursuivrais le mouvement en ligne droite. Mais ce
que je ressens subjectivement, parce que j'ai l'impression "d'aller
tout droit", c'est une 'force' qui me donne
l'impression
d'être expulsé vers l'extérieur.
Cette (pseudo-)force est la
force centrifuge.
Elle n'a pas d'existence physique, d'où le terme 'pseudo-' (qu'il
faudrait systématiquement employer). Elle est
liée au fait que
je
considère subjectivement que je suis 'au centre du monde' et que je me
déplace en ligne droite, soumis à une force, la force
centrifuge, qui tend à m'expulser vers
l'extérieur.
1.2 Forme vectorielle de la vitesse du mouvement circulaire uniforme
De la manière la plus générale possible, une vitesse v, en termes
scalaires, est définie comme la
limite du rapport de la distance parcourue ΔD au temps du déplacement
Δt, c'est-à-dire ΔD / Δt, quand Δt tend vers 0 (Δt → 0).
On
note cette
limite dD / dt, d'où v = dD / dt
Dans
le cas particulier du mouvement circulaire uniforme,
la vitesse (scalaire) v est la quantité constante
v = ds
/ dt
(d'où ds = v
dt)
où ds est
un déplacement infinitésimal sur un cercle (Fig. 1.3).
Comme ds
est égal à R dθ (par définition
même de la notion
d'angle), dθ
étant l'angle
interceptant ds, on peut écrire
v
= R dθ /
dt

Fig. 1.3
La
quantité ω
= dθ / dt est appelée vitesse angulaire:
elle s'exprime en radian s-1 (mais voir note 2)
On a
donc
la relation scalaire
v
= ω R
donc
ω = v / R
où
v, ω et R
sont
constants.
Il est fécond de représenter
la vitesse par le vecteur
vitesse V
(dont l'origine a été placée arbitrairement sur la figure
1.3 'au milieu' de ds):
en effet, une
vitesse a bien un module, une direction et un sens. Il est
intuitivement clair que le
vecteur V,
de module v = |V|,
est
dans le plan du cercle de centre C et qu'il est perpendiculaire au rayon R,
car il est tangent
au cercle.
On
peut
enfin
mettre V sous la forme d'un
produit vectoriel
par la construction
fondamentale suivante :
Soit un cercle de
centre C et de rayon R.
Soit ω
le
vecteur vitesse angulaire
de module |ω|
= ω (en noir
sur la figure 4). Par convention, on lui
impose un direction perpendiculaire
au cercle dans le sens positif (et on
place son origine
en
C).
Soit r =
OA un
vecteur dont l'origine est un point O arbitraire sur la
perpendiculaire au cercle passant par
C et dont l'extrémité est un point A du cercle. O est donc
sur
la droite support de ω.
Considérons
maintenent les deux vecteurs équipollents à ω
et ayant leur origine
en A sur le cercle, donc à l'extrémité d'un rayon R passant par A
(en gris sur la fig. 1.4). Ils sont dans un plan qui
contient R. Soit enfin
γ
l'angle
entre ω
et r.

Fig. 1.4
Comme
R = r sin γ, le
produit vectoriel ω
x r vaut
ω
r sin γ u
, c'est-à-dire ω R u
D'après la définition du produit vectoriel, le
vecteur unité u
est dirigé perpendiculairement au plan
contenant ces
deux vecteurs, donc perpendiculaire à R : il a bien même direction que V, qui est aussi
perpendiculaire à R. On peut
donc écrire en termes
vectoriels
V
=
ω
x r
= ω R u
Notons que si
O est confondu avec C, γ vaut π/2, d'où sin γ = 1, et |r| vaut R. On retrouve bien la
relation scalaire V = ω R.
1.3 Forme vectorielle de l'accélération
du mouvement circulaire uniforme
Nous avons vu que comme
le mouvement circulaire n'est pas rectiligne, il y a nécessairement
intervention
d'une force
faisant varier la direction de V.
L'accélération
A (de module
|A| = a)
est
donné
par définition par la limite de (Vt+Δt
- Vt
) / Δ t quand Δt → 0, notée dV
/ dt
Vt et
V
t+Δt sont notés V1
et V2 à la
figure 1.5.

Fig 1.5
Fig. 1.6
Montrons que l'angle entre les directions de V1
et V2 vaut dθ.
Traçons la droite parallèle à V2
passant par A, qui coupe le rayon CB en D.
Comme l'angle CDA est droit car AD est parallèle à V2, qui est perpendiculaire à CB,
l'angle CAD vaut π/2 - dθ. Comme V1
est perpendiculaire à CA, l'angle entre les directions de V1 et V2 vaut
π/2 - CAD = π/2 - (π/2 - dθ) = dθ.
Construisons maintenent le vecteur différence dV
= V2
- V1 à partir d'un point
arbitraire O (Fig. 1.6)
Le
triangle CAB et le triangle formé pour la construction de dV = V2
- V1
sont semblables :
ils sont tous deux isocèles (|V1|=
|V2|) et
les angles en C et O sont égaux.
Notons dv le module de |dV|
En
assimilant la corde AB et
l'arc de cercle AB, puisque les angles sont
petits, on a les proportions
dv / v = ds / R
Comme ds = v
dt, on peut écrire
dv / v = v dt / R
d'où
on tire que dv / dt, noté a, vaut v² / R
Enfin,
comme v
= R ω, on a, en termes scalaires
a
= v² / R = ω² R
Cette
accélération est dirigée vers le centre du cercle, car l'angle
dθ → 0. Elle est appelée accélération centripète, créée
par une force
dite centrale,
car dirigée vers le centre du cercle.
Montrons maintenant que le vecteur accélération A est égal à ω
x V (=
ω v sin δ u')
où δ est l'angle entre ω et
V (Fig. 1.7)

Fig. 1.7
Comme ω et V sont
perpendiculaires (on a en effet imposé à ω d'être
perpendiculaire au plan contenant le cercle, et V est dans ce plan) , δ
= π/2 et sin δ = 1, donc
A = ω
x V =
ω v u'
u', le
vecteur unité associé à A,
est
perpendiculaire à V, donc le long d'un rayon: il est
bien dirigé vers le centre du cercle, car en tournant de ω à V,
on "visse un
boulon sur la tige filetée" u'
De
plus, v = R ω, d'où
A =
ω
x V
=
ω R ω u'
=
ω² R u'
ce qui
est le résultat cherché.
Comme
V
=
ω x r, on peut aussi
écrire
A =
ω
x (ω x r)
Les
parenthèses sont nécessaires pour interdire d'interpréter ce produit
vectoriel comme (ω
x ω)
x r
qui serait nul, ω
étant parallèle à lui même.
Il
existe une dernière notation simple qui sera utilisée dans les
paragraphes suivants :
On vient de voir que A
est égal à R ω² u',
où u' est le
vecteur
unité orienté de la circonférence vers le centre du cercle.
Soit R le
vecteur rayon,
allant du centre du cercle vers A sur la la circonférence : on a donc R = - R u'.
L'accélération peut alors s'écrire
A
= - ω² R
La (pseudo-)force centrifuge A',
de sens opposé, aura donc pour expression A'
= ω² R
La figure 1.8 et le tableau suivants récapitulent les différents
résultats obtenus.

Fig. 1.8
En termes scalaires
En termes vectoriels
v = ω
R
V
=
ω
x r
= ω R u
a
= v² / R =
ω² R
A = ω
x V = ω
x (ω x r) =
ω² R u' = - ω² R
2 - La force de
Coriolis
: le cas particulier d'un déplacement est-ouest
On
trouve dans le livre de J.R.
Holton 'An Introduction to Dynamic Meteorology' (p. 14 de la
4e édition, 2004), une présentation astucieuse de
la force
de
Coriolis dans le cas particulier d'une corps se déplaçant vers l'est
(ou l'ouest) à
la surface de la terre.
Considérons une particule
de masse
unité pouvant se
déplacer (sans friction) à la surface de la Terre. Dans
ces conditions,
F = accélération.
Soit Ω la
vitesse
angulaire de la Terre, qui tourne vers l'est, et r
le vecteur position 'horizontal', c'est-à-dire dans le plan du cercle
de latitude, allant de l'axe de rotation du globe à
la
particule (voir fig. 2.3). (Le symbole Ω est usuel en météorologie).
Le module de r vaut R cos
Latitude, avec R le rayon
terrestre (R ≈ 6370 km = 40 000 km / 2*π ). A la latitude
45° par exemple, r ≈ 4500 km (= 6370 cos (π/4)).
Lorsque la
particule est au repos par rapport à
la Terre, les seules forces
agissant sur cette masse, du
point de vue d'un
observateur sur Terre, sont la force de gravité
et la (pseudo-)force
centrifuge F
= Ω²
r, liée à la
rotation de la Terre, car cette particule tourne le long d'un
cercle de rayon r.
Supposons maintenant que cette
même particule soit en mouvement vers
l'est (donc dans le même sens que la rotation de
la Terre) à une vitesse constante non nulle v (fig. 2.3).
Comme la particule
tourne maintenant autour du globe à une vitesse
supérieure à la vitesse de la rotation de la Terre, la force centrifuge
est plus importante.
Cette vitesse angulaire supplémentaire ω étant égale à v / r, la
force centrifuge totale vaut donc
(Ω + ω)² r = (Ω + v / r)² r = Ω²
r +
(v² / r²) r +
(2 Ω v / r) r
• Le
premier terme, Ω² r,
est
la force centrifuge par unité de masse due à la rotation uniforme de la
Terre.
A l'équateur, un point décrit un cercle d'environ 40 000
km en 24 h, soit une vitesse vEq d'environ 465 m/s (1674
km/h). L'ordre
de
grandeur de ω = vEq / R est donc de 7 x 10-5
rd / s. Pour
une masse unité, la force centrifuge à l'équateur valant vEq²
/ R ,
l'ordre de grandeur est de 0,03 N, soit une diminution d'environ 3
grammes pour une masse de 1 kg. On notera
que cette force
centrifuge n'est PAS orientée le long de la verticale
du lieu z sauf à l'Equateur (voir Fig. 2.3). Elle
fait un angle égal à la latitude avec
la verticale du lieu, donc un angle π/2 - Lat avec l'horizon h, en
direction du sud dans l'hémisphère nord.
L'effet de la force centrifuge est maximal à
l'équateur, et
nul aux pôles. Ajouter vectoriellement à g*, notation classique de
la force
gravitationnelle due à la seule masse de la Terre, cette force
centrifude définit g,
notation classique de la
force gravitationnelle "effective", qui définit à son tour la surface
de
l'ellipsoïde du globe terrestre, qui lui est en tout point
perpendiculaire (fig. 2.1) (voir note 3). A la latitude 45°, g diffère de g* d'environ un
dixième de degré.
Les
mesures expérimentales montrent que
cette
force centrifuge rend compte d'un peu plus de la moitié de la variation
observée de la valeur de g (9,83
N/kg aux pôles contre 9,78 N/kg
à l'équateur, soit une différence d'environ 0,05 N, 5 grammes pour une
masse de 1 kg). C'est la non-sphéricité de la Terre, un
rayon équatorial mesurant en effet environ 21
km de plus qu'un rayon polaire, qui est responsable du reste. C'est
d'ailleurs l'action de la force centrifuge sur un Terre encore
plastique au début de sa formation qui explique cet aplatissement aux
poles et ce gonflement à l'équateur.

Fig 2.1
L'analyse détaillée des valeurs de la gravité en de
très nombreux points du globe permet enfin de mesurer la forme exacte
de la Terre, ou géoïde, qui ne
diffère de l'ellipsoïde que par un
ensemble de 'bosses' et 'creux' d'au plus une centaine de mètres (Fig.
2.2). Les GPS tiennent compte de l'altitude du géoïde par rapport à
l'ellipsoïde WGS84 dans le calcul de l'altitude d'un lieu.
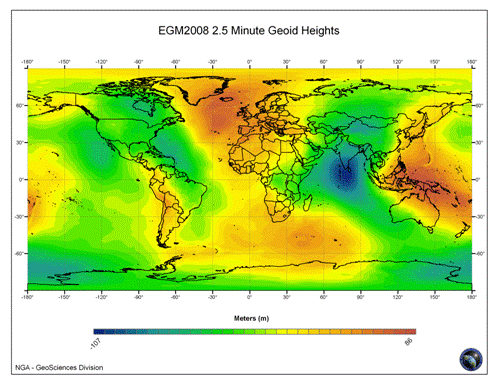
Fig. 2.2
Les deux autres termes de la relation représentent des
forces 'déflectrices', agissant vers l'extérieur du globe, dans
la
direction de r.
•
Si ω = v / r est petit par
rapport à Ω, le
terme en (v / r)² est
négligeable.
La circonférence décrite en 24 h dans un lieu à 45° de
latitude vaut 28000 km environ, ce qui correspond à
une vitesse d'environ 1170 km /h (325 m/s). Une vitesse de quelques
dizaines
de km/h (30 km = 8 m/s) , typique pour les phénomènes météorologique,
est effectivement
faible de ce point de vue. Le rapport (v / r)² est
dans ce cas de l'ordre de 6 x 10-4.
• La force C
= (2 Ω v
/ r) r
par unité de masse est la force
de Coriolis.
Elle est dans le plan du
cercle de latitude. Son module
vaut
(2 Ω v / r) r = 2 Ω v (La
dimension de cette force par unité de masse est bien celle d'une
accélération : (T-1) ( LT-1)
(L-1) (L) = L T-2 )


Fig. 2.3
La
force de Coriolis peut être décomposée en deux vecteurs, l'un vertical,
vers le zénith de la position de la particule, et l'autre dit
méridional, vers l'horizon du lieu, dans une direction
nord-sud.
Dans la direction du zénith, le
module de la force de Coriolis vaut 2 v Ω cos
Lat. Cette composante tend à 'alléger' la
particule se déplaçant vers l'est.
Dans la direction méridienne, le
module de la force de Coriolis pour une masse unité vaut 2 v Ω sin
Lat.
Cette force est dirigée
vers le sud, à 'droite' donc de la trajectoire vers l'est.
Notons que cette composante est nulle à l'équateur (Lat = 0°,
car sin Lat = sin 0 = 0)
La magnitude de la composante méridionale de la force de Coriolis est
de l'ordre de
10-2 ms-2,
mille fois plus petite que celle liée à l'accélération de la pesanteur
(environ 10 ms-2).
Mais son application pendant des heures, ou même des jours, produit une
déviation marquée de la trajectoire d'un phénomène météorologique comme
le vent soufflant d'une zone de haute pression vers une zone de basse
pression.
• Il est facile de montrer que si le mouvement de la
particule se fait en sens inverse, vers l'ouest, la force méridienne
est dirigée vers le
nord (Fig. 2.4). En effet,
(Ω - ω)² r
= (Ω - v / r)² r
= Ω² r
+ v² / R² r -
(2 Ω v / r) r

Fig. 2.4
La force de Coriolis est dans ce cas orientée vers l'axe de rotation de
la Terre.
La composante verticale, orientée vers le centre de la Terre, tend à
'alourdir' la particule. La composante méridienne est orientée vers le
nord, toujours à droite de la
trajectoire.
• Dans le cas d'un mouvement vers le nord ou le
sud, il existe une autre
présentation faisant appel à la notion physique de conservation du
moment cinétique. On montre que la force
de Coriolis est orientée vers l'est quand le déplacement est vers le
nord, et vers l'ouest quand il se produit vers le sud (voir §5 plus bas)
En résumé, toute particule en mouvement dans l'hémisphère nord est
déviée vers sa droite, et vers sa gauche dans l'hémisphère sud.
Nous allons maintenant poursuivre pour donner une présentation plus
générale.
3 - Rappel :
le
mouvement
relatif
Nous
allons voir que la
description d'un mouvement dépend du système de référence (ou système
d'axes) choisie par
l'observateur.
Comme deux observateurs peuvent choisir des systèmes de
référence différents, il est crucial de savoir transformer les
descriptions faite à partir d'un système à celles faites à partir d'un
autre afin de décider s'il
s'agit par exemple du même mouvement.
Beaucoup
d'observations faites sur terre le sont dans un système lié à la terre,
qui se déplace donc avec elle. Nous verrons que la description n'est
pas la même
si elle est faite à partir de point fixe de l'espace, où la terre est
un objet tournoyant sur lui-même.
3.1 - Vitesse et accélération
relative
Avant
d'entrer dans le vif du sujet, il faut définir ce qu'on appelle vitesse
et accélération relative.
Considérons
deux objets A et B et un observateur en O utilisant comme système de
référence les axes OX, OY et OZ de la figure 3.1.
Par rapport
à O, la position des objets est donnée par les vecteurs rA
et rB.
Les deux objets ont par définition pour vitesse VA
= drA
/ dt et VB
= drB
/ dt
On appelle vitesse
relative de B par rapport à A VBA la
variation du
vecteur rBA
= rB
- rA
d'origine A et d'extrémité B : VBA
= drBA
/ dt

Fig. 3.1
De
même, la vitesse relative de A par rapport à B
VAB est donnée par
la variation du vecteur rAB
= - rBA
= rA
- rB
d'origine
B et et d'extrémité A :
VAB
= drAB
/ dt
Comme rAB
= - rBA
, on a
VBA = - VAB
La
vitesse de B par rapport à A est égale et opposée à la vitesse de A par
rapport à B.
Soit
une personne A sur un quai faisant face à une personne B
dans un train qui démarre. Elles fixent (arbitrairement) le sens
positif vers la droite de A : A tient une flèche dans le sens positif,
donc vers sa droite. Si A voit B partir sur sa droite, dans le
sens
positif de la flèche à une vitesse VBA,
alors B voit A partir dans le sens inverse de celui de la
flèche, le sens négatif, à une vitesse opposée VAB
= - VBA.
On
peut obtenir la vitesse relative de B par rapport à A en dérivant par
rapport au temps rBA
= rB
- rA
drBA
/ dt = drB /
dt - / drA
/ dt = VBA
= VB
- VA
En
dérivant par rapport au temps
rAB = rA
- rB
on obtient la vitesse relative de A par rapport
à B
drAB
/ dt = drA
/ dt - / drB
/ dt = VAB
= VA
- VB
et on a bien VBA
= - VAB
Donc,
pour obtenir la vitesse relative de deux corps, on soustrait leurs
vitesses par rapport à l'observateur.
D'une
manière similaire, on peut obtenir l'accélération de B par rapport à A,
noté aBA,
en dérivant VBA
= VB
- VA
aBA
= dVBA /
dt = dVB
/ dt - dVA
/ dt
Les termes du second membre sont l'accélération de B et
l'accélération de A, aB
et aA,
d'où
aBA
= aB
- aA
On
aura de même
aAB
= aA
- aB
Donc,
pour obtenir l'accélération relative de deux corps, on soustrait leurs
accélération par rapport à l'observateur.
3.2 - Mouvement relatif uniforme
de
translation
Considérons
deux observateurs O et O' qui se déplacent l'un par rapport à l'autre
d'un mouvement de translation uniforme (c'est-à-dire qu'ils ne tournent
pas l'un par rapport à l'autre). L'observateur O voit donc
l'observateur O' se déplacer à la vitesse v, alors que O' voit
O se déplacer à la vitesse - v.
Nous voulons comparer leur description d'un objet mobile.
Pour
des raisons de simplicité, choisissons comme axe OX et OX' la droite du
mouvement relatif, et les axes OY et OY', ainsi que OZ et OZ'
parallèles entre eux (fig. 3.2).

Fig. 3.2
Nous
supposerons qu'au temps t = 0, O et O' sont confondus. En appelant v la vitesse
relative constante, nous avons alors OO'
= vt.
Soit
un objet au point A, avec
OA = r,
et O'A = r'. On a OA = OO' +
O'A soit r =
vt + r', ou encore
r'
= r - vt
Cette relation vectorielle peut être décomposée
selon ses trois composantes, en tenant compte du fait que v est parallèle a
OX.
x'
= x - vt
y' = y
z = z'
C'est la
transformation de Galilée
(qui
présuppose, il faut le noter, t = t', l'invariance du temps
pour
deux observateurs en mouvement relatif uniforme de translation)
La
vitesse V
de A par rapport à O est définie par
V
= dr / dt
La
vitesse V'
de A par rapport à O' est définie par
V'
= dr' /
dt
Comme r'
= r - vt
, avec v constant, V' peut encore
s'écrire V'
= d(r - vt
) / dt
= dr
/ dt - v
d'où
V' = V
- v
Cette
équation (ou son équivalent en termes de composantes : V'x = Vx - v ;
V'y = Vy; V'z = Vz) donne la règle de Galilée pour comparer
les
vitesses d'un objet mesurées par deux observateurs en mouvement relatif
de translation
Si A se déplace parallèlement à OX, alors nous
avons simplement V' = V - v
Calculons maintenant les
accélérations.
L'accélération de A par rapport à O est a = dV
/ dt
L'accélération
de A par rapport à O' est a'
= dV' / dt
Comme
V'
= V
- v, a' = dV
/ dt - v / dt.
Comme v est
constant, on obtient a'
= dV / dt et
a = a'
Les
deux
observateurs en mouvement relatif uniforme de translation mesurent la
même accélération
L'accélération
reste invariante quand on passe d'un système de référence à un autre
qui est en mouvement uniforme de translation par rapport au premier.
4 - Mouvement relatif
uniforme
de
rotation : la
force de Coriolis
Inspiré de la démonstration sur http://www.sciences.ch/htmlfr/mecanique/mecanclassique02.php
Considérons
un référentiel fixe X, Y,
Z d'origine O et un référentiel mobile xyz
d'origine o en mouvement relatif.
Il
s'agit d'exprimer la vitesse et l'accélération d'un point P
de l'espace au moyen des coordonnées ( = composantes) liées au
référentiel fixe
(coordonnées dites absolues) à partir des coordonnées liées au
référentiel mobile (coordonnées dites relatives) et du mouvement
(dit mouvement d'entraînement) du référentiel mobile. Nous
envisagerons particulièrement une rotation du référentiel mobile xyz.
(Fig. 4.1).

Fig. 4.1
• La
position
du
point P est donnée par une "relation
de composition des position"
Soit ro
le vecteur de position de o
par rapport à
l'origine du référentiel fixe O
Soit r est
le vecteur de
position de P par rapport au référentiel mobile
ra
est
le vecteur de position de P par rapport
au
référentiel fixe
P a pour composante x, y et z dans le
référentiel mobile (r
(= oP)
= xi
+ yj + zk)
Si P se
déplace en fonction du temps, x, y et z sont des fonctions du temps :
x = x(t), y = y(t) et z = z(t).
On a
ra
= ro
+ r
4.1 Vitesse absolue
La
vitesse absolue va
de P est par définition
va
= dra
/ dt
= d(ro +
r) / dt
= dro /
dt + dr / dt
= dro /
dt + d(xi + yj + zk)
/ dt
va
= vo
+ d(xi + yj + zk)
/ dt
vo
=
dρ / dt est
la vitesse
dite d'entraînement
du référentiel mobile : c'est la
vitesse de déplacement
du référentiel xyz par rapport à O.
Si le
référentiel xyz est en
rotation, i,
j et k varient
en fonction du temps et il faut les traiter comme des fonctions : i = i(t),
j = j(t) et k = k(t)
Le
second terme est alors la dérivée d'une somme de
produits de
fonctions de t (cf. d(f(x)g(x)) / dx = f'(x)g(x) + g'(x)f(x))
d'où
d(xi
+ yj + zk) / dt = (dx/ dt i
+ dy / dt j
+ dz / dt k)
+ (x di / dt
+ y dj/ dt +
z dk / dt)
et
va = vo
+ (dx/ dt i
+ dy / dt j
+ dz / dt k)
+ (x di / dt
+ y dj/ dt +
z dk / dt)
La
second terme représente la vitesse
relative vr,
c'est-à-dire la vitesse de P par rapport au référentiel mobile xyz
(cette vitesse
est supposé connue),
d'où
va = vo
+ vr
+ (x di / dt
+ y dj / dt
+
z dk / dt)
Le
dernier terme est la contribution à la vitesse absolue de la rotation
du référentiel mobile.
Il s'agit maintenant d'exprimer la
valeur de cette contribution.
Posons di, dj et dk en termes de
composantes
di
/ dt = a i
+ b j + c k
dj / dt
= d
i + e j + f k
dk
/ dt = g
i + h j + i k
Il est
certain que les valeurs de ces composantes ne sont pas indépendantes
car i, j et k restent toujours
perpendiculaires deux à deux.

Fig. 4.2
A - On peut
noter (Fig. 4.2) que di
/ dt est
perpendiculaire à i,
d'où i di / dt = 0. On a de
même j dj / dt et k dk
/ dt
d'où
i
di / dt = i(a i + b j + c k) = a = 0
j dj / dt = j(d i + e j + f k)
= e = 0
k dk / dt = k(g i + h j + i k) = i = 0
et
di / dt
= b
j + c k
dj / dt
= d
i + f k
dk
/ dt
= g i
+ h
j
B
- On peut noter que i
dj / dt = - j di / dt car si
l'angle entre i
et dj / dt
vaut α, l'angle entre dj
/ dt et i
vaut (π - α), d'où i
dj /dt + j di
/ dt = 0
On
a de même i
dk /dt + k di
/ dt = 0 et j dk /dt + k dj
/ dt = 0
d'où
i dj
/dt + j di / dt = 0 = i(d i
+ f k) + j(b
j + c k) = (d + b),
d'où d = - b
i
dk /dt + k di
/ dt = 0 = i(g i + h
j) + k(b
j + c k) = g + c, d'où c =
- g
j
dk /dt + k dj
/ dt = 0 = j (g i + h
j) + k (d
i + f k) = h + f, d'où h =
- f
d'où
di
/ dt
= b
j - g k
dj / dt
= -b
i + f k
dk
/ dt
= g i
- f
j
On
a donc
(x di
/ dt
+ y dj / dt
+
z dk / dt)
= x(b
j - g k)
+ y(-b i + f k) + z(g i - f
j) =
i (gz - by
) + j (bx -
fz
) + k (fy -
gx)
En posant ω
= (fi +
gj + bk) = ( ωxi + ωyj +
ωzk)
, il est
clair que (x di
/ dt
+ y dj / dt
+
z dk / dt)
est le produit vectoriel
ω x
r
Ce résultat n'est pas surprenant quand on regarde la figure 4.3
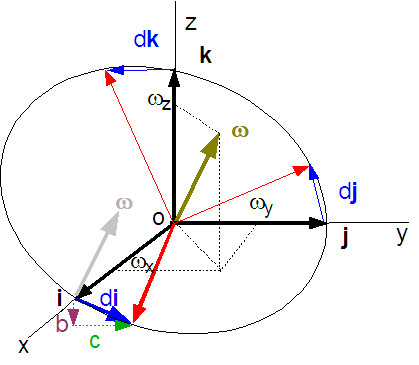
Fig. 4.3
On voit que di
/ dt se construit comme une vecteur vitesse. Il vaut donc ω
x i.
On obtient finalement
va = vo
+ vr
+
ω x r
La vitesse
absolue va est égale à la
somme
- de la vitesse
d'entraînement vo du
référentiel mobile,
- de la vitesse du point vr dans
le
référentiel mobile et
- de la vitesse de rotation ω
x r du
référentiel mobile.
On
constate, comme nous le savons déjà, que si la vitesse de rotation est
nulle (ω
= 0), la vitesse absolue est égale à la vitesse d'entraînement du
référentiel mobile et de la vitesse du point dans le référentiel mobile
: va =
ve
+ vr
(transformation de Galilée).
4.2 Accélération absolue et force
de Coriolis
On
peut maintenant chercher le rapport entre l'accélération absolue
et les
accélérations découlant du déplacement du référentiel mobile.
Par
définition
aa =
dvo
/ dt + dvr/dt
+ d(ω x
r)
/ dt
- On peut écrire immédiatement d(vo)
/ dt
= ao
car on est dans le repère fixe.
- Le dernier terme
vaut d(z ωy
- y ωz)
i / dt +
d(x ωz - z ωx )
j / dt +
d(y ωx - x ωy)
k / dt
Sachant
que x, y et z, les coordonnées de ω
ainsi que i, j et k, sont des
fonctions du temps, un
développement pénible
donne
d(z
ωy
- y ωz)
i / dt +
d(x ωz - z ωx )
j / dt +
d(y ωx - x ωy)
k / dt =
dz / dt ωy
i +
dωy / dt z i
+ di
/ dt z ωy
- dy / dt ωz i
- dωz
/ dt y i
- di
/ dt y ωz
+
dx / dt ωz j + dωz
/ dt x j
+ dj
/ dt x ωz
- dz / dt ωx j
- dωx
/ dt z j
- dj
/ dt z ωx
+
dy / dt ωx k + dωx
/ dt y k
+ dk
/ dt y ωx
- dx / dt ωy k
- dωy
/ dt x k
- dk
/ dt x ωy
On
peut regrouper les termes en dx / dt, dy / dt et dz / dt
dz
/ dt ωy
i - dy / dt ωz i
+ dx /
dt ωz
j - dz / dt ωx j + dy /
dt ωx
k -
dx / dt ωy
k
=
(dz / dt ωy -
dy / dt ωz) i + (dx /
dt ωz
- dz / dt ωx) j +
(dy /
dt ωx - dx / dt
ωy)
k =
ω x vr
On peut regrouper
les termes en dω
dωy / dt z i
- dωz
/ dt y i +
dωz / dt x j
- dωx / dt z j
+ dωx
/ dt y k -
dωy / dt x k
=
(dωy / dt z -
dωz
/ dt y) i +
(dωz / dt x
- dωx / dt z) j
+ (dωx
/ dt y - dωy
/ dt x) k =
dω / dt x r
Il
reste à regrouper les termes en du
/ dt
di
/ dt z ωy
- di / dt y ωz
+ dj / dt x ωz -
dj / dt z ωx + dk
/ dt y ωx
- dk / dt x ωy
=
di / dt (z ωy
- y ωz)
+ dj / dt (x ωz - z ωx) + dk
/ dt (y ωx
- dk / dt x ωy)
On
sait qu'on a
di
/ dt = ωz j - ωy k
dj /
dt = ωx k
- ωz i
dk /
dt = ωy i
- ωx j
d'où
(ωz j - ωy k) (z
ωy - y ωz)
+ (ωx k
- ωz i) (x ωz - z ωx) + (ωy i
- ωx j) (y
ωx - x
ωy)
= ωz
(z
ωy - y ωz)
j - ωy (z
ωy - y ωz)
k + (ωx (x ωz - z ωx) k
- ωz (x ωz - z ωx) i
+ (ωy (y ωx
- x ωy) i
- ωx(y ωx
- x ωy)
j
= (ωy - ωz )(y
ωx - x
ωy) i + (ωz - ωx)(z ωy
- y ωz)
j + (ωx
- ωy ) (x ωz - z ωx) k
= ω x (ω x r )
L'accélération absolue s'écrit à ce stade
aa =
ao
+ dvr
/ dt
+ ω x vr + dω / dt x r + ω x (ω x r )
Reste
à calculer dvr
/ dt : on sait que vr = dx / dt i + dy / dt j + dz / dt k
d'où
dvr
/ dt = d / dt (dx / dt i
+ dy / dt j
+ dz / dt k)
Sachant que i,
j et k sont fonctions du
temps
dvr / dt = (d²x / dt² i
+ d²y / dt² j + d²z / dt² k) + (dx / dt di / dt + dy / dt dj / dt + dz / dt dk / dt)
= ar + ω dr
/ dt = ar + ω x vr
L'accélération
absolue est donc donnée par
aa =
ao
+ ar + 2
ω x vr + dω / dt x r + ω x (ω x r )
On reconnait
- L'accélération centripère ω x (ω x r )
- L'accélération dite de Coriolis 2
ω x vr ,
du
nom du physicien l'ayant identifié pour la première fois.
-
un dernier terme qui dépend de
la dérivée temporelle de ω.
Si ω est constant dans le
temps, ce qui est le cas de la rotation terrestre, ce terme est nul.
Notons
dès maintenant que si ω
= 0 , l'accélération
absolue vaut aa =
ao
+ ar.
De plus, si les
observateurs sont en mouvement
relatif uniforme de translation, ar
est
nul, et ils mesurent la
même accélération : aa = ar
5 -Moment angulaire,
cinétique et d'inertie
Ces notions sont indispensables pour comprendre pourquoi, dans
l'hémisphère nord, un objet de déplaçant vers le nord est dévié vers
l'est par la force de Coriolis, alors qu'il dévié vers l'Ouest s'il se
dirige vers lesud.
1 - Moment angulaire (torque)
τ ≡ r × F
La valeur scalaire (c'est-à-dire
numérique) du moment angulaire
τ (tau) d'une force (anglais US torque, britannique moment) est
définie comme le produit
- de la valeur d'une force F⊥
appliquée perpendiculairement
sur un levier
par
- la distance r appelée 'bras
de levier' entre
le point d'application de la force et le pivot du levier (Fig. 5.1).
τ ≡
r F⊥

Fig.
5.1
Mais pour
utiliser pleinement la notion de moment angulaire, il est (presque)
indispensable de définir le moment angulaire comme un vecteur.
• Le vecteur moment angulaire est défini
comme le produit vectoriel
d'une force F par le vecteur
position r
entre le pivot et le point d'application de la force (Fig.5.2).
La
direction du vecteur moment angulaire est de ce fait perpendiculaire au
plan contenant r et F
Sur la figure 5.2, nous
avons placé arbitrairement l'origine du vecteur moment angulaire sur le
pivot; ce
vecteur n'a pas d'existence physique et ne représente certainement pas
une force.
τ ≡ r × F


Fig. 5.2
Fig. 5.3
L'orientation de la force détermine le 'sens de rotation' du levier. Le
sens positif (négatif) du vecteur est le sens utilisé pour (dé)visser
un écrou sur le vecteur moment angulaire vu comme une tige filetée: il
est
positif sur les figures 5.2 et 5.3 et négatif sur la figure 5.4.
De la définition du produit vectoriel, on tire immédiatement que le
module du moment angulaire est donné par
τ = r F sin θ
où θ est l'angle entre le vecteur position
r et la force F (Fig.
5.2, Fig 5.3).
Si la force F est perpendiculaire au bras de levier (F⊥), on
retrouve bien la première définition τ = r F, car
sin(π/2) = 1.

Fig. 5.4
On en déduit immédiatement qu'une force parallèle au vecteur position
ne produira pas de moment car sin (0) (et sin (π)) sont nuls. C'est
évidemment le cas lorsque les supports des vecteurs r et F sont
confondus (Fig. 5.5)
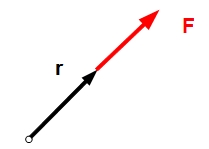
Fig. 5.5
Intuitivement en effet, une force exercée dans la direction du levier
ne peut pas faire pivoter celui-ci.
2 - Moment cinétique (angular momentum)
L ≡ r
× m v
τ = dL/dt
L
= m r2 ω
Il
est fécond de définir la notion de moment
cinétique (anglais angular
momentum) en lien avec la notion de quantité de mouvement.
• Rappel: la quantité de mouvement
Une force, qui est le produit d'une masse par une accélération, peut
également être définie comme le taux de variation
(c'est-à-dire la dérivée temporelle) d'une quantité vectorielle p appelée
quantité de mouvement (anglais
momentum), le produit de la
masse m d'une particule par sa vitesse v
p = m
v
La force F impliquée est alors donnée par
F ≡ dp/dt
= d(m v)/dt
Si la masse m est constante
F = m dv / dt = m a
où l'on retrouve bien la caractérisation d'une force comme le produit
d'une masse par une accélération.
• D'une manière parallèle, on
peut définir un moment angulaire comme le
taux de variation (ou dérivée temporelle) d'une quantité vectorielle L, appelée moment cinétique, qui est le produit
vectoriel d'une vecteur position r
(le bras de levier) par la quantité de mouvement p = m v d'une particule.
L ≡ r × p
≡ r × m v
d'où en termes scalaires L = r m v sin(r,
v)
•
On peut montrer que le moment angulaire est la dérivée temporelle du
moment cinétique
τ = dL/dt
mais la démonstration n'est pas immédiate. Nous la donnons au bas de
cette page.
La variation dL
du moment cinétique pendant un très court intervale de temps est donc
parallèle
au moment τ appliqué
à la particule. D'autre part, le vecteur moment cinétique est
perpendiculaire au plan contenant les vecteurs r et v.
La figure 5.6 illustre le
moment
cinétique L
par rapport à un point O d'une particule de masse m se déplaçant à la
vitesse v,
possédant donc une quantité de mouvement p = m v. Son origine a été placé
arbitrairement en O sur la figure.
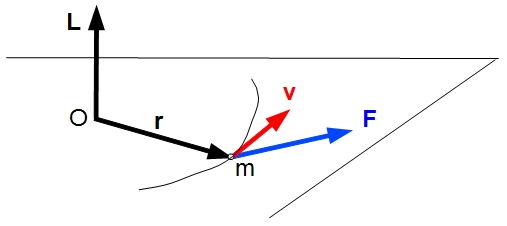
Fig.
5.6
Le moment cinétique d'une particule peut changer de module et /
ou de direction lors du déplacement de la particule, en
raison de la modification
du module ou de l'orientation de r
et/ou de v.
• Moment cinétique (angular momentum) dans le mouvement circulaire
Dans le cas important d'un mouvement
circulaire de centre O et de rayon R, les vecteurs v
et R sont
perpendiculaire (Fig.5.7).
On a donc
L = R
x m v = R mv sin (R,v)
= R mv
(car sin (R,v)
= sin (π/2) = 1)
Comme v = ω × R, d'où scalairement v = ω R dans le
cas où ω et R sont perpendiculaires, on peut donc écrire scalairement
L
= R m (ω R) = m R2 ω
La direction de L ≡ R
× m v, perpendiculaire donc au
plan contenant R et v, est la même que celle de ω, d'où vectoriellement
L
= m R2 ω

Fig.
5.7
On notera que dans le mouvement circulaire, ω = dθ / dt et r sont
constants, d'où L
constant.
• Si le moment angulaire appliqué à une particule
est nul (τ = r × F
= 0), nous avons τ = dL / dt = 0 et
L est alors un vecteur
constant.
Le moment cinétique L d'une particule est donc constant
si le moment angulaire τ des forces appliquées est nul.
En d'autres termes, si le moment angulaire des forces appliquées est
nul, il y a conservation du moment
cinétique.
On notera le parallèle avec la conservation de la quantité de mouvement
pour une particule libre.
Le moment angulaire τ appliqué
à une particule est également nul si F
= 0, c'est-à-dire si la particule est libre, se déplaçant de manière
rectiligne à vitesse constant (Fig 5.8).

Fig. 5.8
On a dans ce cas
L = m v r sin θ
Or d = r sinθ, donc L = m v d. Cette quantité est
constante, car tout les facteurs sont constants: en particulier, d est
invariant, même lorsque r
et θ varient.
• La condition τ
= r
× F = 0 est
également remplie lorsque F est parallèle à r,
c'est-à-dire lorsque la direction de F
passe par O, origine du vecteur r.
Une
force dont la direction passe toujours par un point fixe est appelée force centrale. (Fig. 5.9)

Fig. 5.9
Lorsqu'un corps se déplace sous l'effet
d'une force centrale, son
moment cinétique L reste constant. La réciproque est
également vraie.
Quand
la force est centrale, le moment cinétique par rapport au centre de la
force est une constante, et réciproquement
Ce résultat est important car beaucoup de forces dans la nature sont
des forces centrales: par exemple la Terre se déplace par rapport au
Soleil sous l'influence d'une force centrale. Le moment cinétique de la
Terre par rapport au Soleil est donc constant.
•
Pour être complet, ajoutons que si le mouvement n'est pas circulaire
mais curviligne, on
peut
décomposer la vitesse suivant sa composante radiale vr
(vers O) et transversale vθ (Fig. 5.10)
Seule la composante
transversale vθ = r (dθ / dt) contribue
au moment cinétique, d'où
L = mr2
dθ / dt
Si dans le mouvement circulaire L
est constant, ce n'est pas le cas du mouvement curviligne, où L est variable.
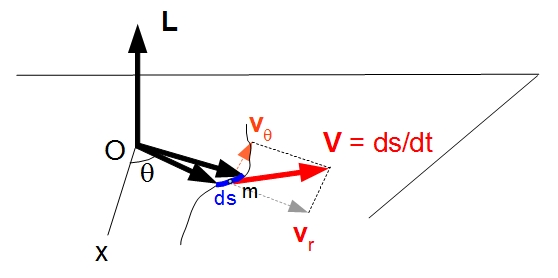
Fig.
5.10
3 - Moment d'inertie (moment of inertia) et énergie cinétique
I ≡ m r2
L = I ω
Rappel: énergie cinétique
•
La notion d'énergie cinétique d'une particule résulte de la définition
du travail d'une force comme
le produit scalaire de cette force par la
distance parcourue par la
particule
Le travail élémentaire dW
d'une force F est défini par
dW ≡ F.dr
où dr est la distance parcourue
par la particule.
Comme F = m dv / dt et dr = v
dt, le travail W entre deux positions a et b est donné par l'intégrale
W = m ∫ab (dv / dt) v dt = m ∫ab
v dv
= 1/2 m (vb2 - va2) = 1/2 m
vb2 - 1/2 m va2
La quantité
Ec = 1/2 m v2
est appelée énergie cinétique
de la particule.
Le travail W d'une force entre deux positions est donc la différence
entre l'énergie cinétique de la particule au point d'arrivée et
l'énergie cinétique
au point de départ:
W = Ec,b - Ec,a
•
Calculons maintenant l'énergie
cinétique Ec = 1/2 m v2 d'une particule de
masse m sur une trajectoire circulaire
de rayon r autour d'un point O.
La vitesse V peut s'exprimer par V = r ω, d'où
Ec = 1/2 m r2 ω2
•
Définissons le moment d'inertie
I comme la quantité m r2
I ≡ m r2
On a donc, dans le mouvement circulaire
Ec = 1/2 I ω2
Dans le mouvement circulaire, I joue donc formellement le rôle de m dans le calcul de
l'énergie cinétique Ec = 1/2 m v2
•
Dans le cas du mouvement circulaire, il existe une relation simple entre le moment cinétique et le moment d'inertie.
Nous avons vu que
L = m r2 ω
Le moment cinétique peut donc s'écrire
L = I ω
A ce stade de l'exposé, les manuels de physique developpent le
calcul du moment d'inertie pour des objets de forme géométrique simple:
disque, anneau, cylindre, cube, sphère etc...
dL
/ dt = τ : démonstration
L ≡ r ×
p = m r × v
Soit L' = r × v = (ri
+ rj + rk) ×
(vi + vj + vk)
L' = (ri
+ rj + rk) ×
(vi + vj + vk)
= ri x
vi + ri x vj
+ ri x vk + rj x
vi + rj x
vj + rj x
vk + rk x
vi + rk x
vj + rk x
vk
=
ri x vj
+ ri x vk
+ rj x vi
+ rj x vk
+ rk x vi
+ rk x vj
=
ri.vj k - ri.vk j - rj vi k
+ rj.vk i + rk.vi j - rk.vj i
= (rj.vk - rk.vj) i + (rk.vi - ri.vk) j + (ri.vj - rj vi) k
-----------------
j
k
i (anti-)horaire -(+)
-----------------
Les vecteurs r et v sont implicitement fonctions du
temps: r(t), v(t)
dL'/dt = rj dvk/dt i + drj/dt vk i - rk dvj/dt i - drk/dt vj i + rk dvi/dt j + drk/dt vi j - ri dvk/dt j - dri/dt vk j + ri dvj/dt k + dri/dt vj k - rj dvi/dt k - drj/dt vi k
= (drj/dt vk - drk/dt vj) i +
(drk/dt vi - dri/dt vk) j + (dri/dt vj - drj/dt vi) k
(= dr/dt × v = (dri/dt i + drj/dt j + drk/dt k) × (vi
+ vj + vk) = (drj/dt vk - drk/dt vj) i + (drk/dt vi - dri /dt vk) j + (dri/dt vj - drj/dt vi) k)
+ (rj dvk/dt - rk dvj/dt) i + (rk dvi/dt - ri dvk/dt) j + (ri dvj/dt - rj dvi/dt) k
(= r × dv/dt) = (ri
+ rj + rk) × (dvi/dt i + dvj/dt j + dvk/dt k) = (rj dvk/dt - rk.dvj/dt) i + (rk.dvi/dt - ri.dvk/dt) j + (ri dvj/dt - rj dvi/dt) k )
dL'/dt = d(r × v)/ dt = (dr/dt × v) + (r × dv/dt)
dL/dt
= d(r × mv)/ dt = (dr/dt × m v) + (r × m dv/dt)
Or (dr / dt)
× mv = v × mv
= 0 (car v
est colinéaire à
lui même !)
Il reste donc
dL
/ dt = r × m dv / dt = r × m a = r
× F
Or τ ≡
r × F
d'où
dL
/ dt = τ
Notons que cette relation n'est valide que si L et τ sont mesurés par
rapport au même point O
4
- Application au calcul de la force
de Coriolis dans le cas d'un mouvement nord/sud
On vient de voir que le moment cinétique I d'une masse unité en
rotation à vitesse constante à une distance r du point de pivotement
vaut r2Ω
Le raisonnement est le suivant: dans l'hémisphère
nord, dans le cas d'un déplacement le long de la surface du
globe (ou déplacement 'horizontal') d'une masse unité à
vitesse constante v vers le sud,
la distance
au centre de rotation augmente (voir figure 5.11). Comme I est invariant
en raison de l'absence de force dirigée dans le sens est ou ouest
(c'est-à-dire en l'absence de moment angulaire appliqué à la
particule) il faut que la
vitesse de rotation diminue,
ce qui implique un mouvement vers l'ouest pour un observateur qui se
trouve sur la terre. La vitesse initiale de rotation Ω sera donc
modifiée
d'une valeur ω = dv/(r + dr), dirigée vers l'ouest
Pour un déplacement vers le nord, la distance au centre de
rotation diminue. L'invariance de I implique donc une accélération de
la vitesse de rotation, donc un mouvement vers l'est.
La conservation de I implique donc
I = r2Ω
= (r + dr)2 (Ω + dv/(r + dr)) = (r2 + 2dr r + dr2)(Ω
+ dv/(r + dr)) = r2 Ω + 2dr r Ω + dr2Ω + r2
dv/(r + dr) + 2dr r dv/(r + dr) + dr2 dv/(r + dr)
Au premier ordre, c'est-à-dire en ne conservant que les termes ne
comportant au plus qu'une unique différentielle de degré un
I = r2Ω
= r2 Ω + 2dr r Ω + r2 dv/(r + dr)
Il faut donc que la somme des deux derniers termes soit nulle
2dr r Ω + r2 dv/(r + dr) = 0
c'est-à-dire
r2 dv/(r + dr) = - 2dr r Ω
La différentielle de vitesse dv vaut alors
dv = - 2dr r Ω (r + dr) / r2
= - 2dr r Ω r/r2
- 2dr r Ω dr / r2
En ne conservant à nouveau que le terme de premier ordre, on obtient
dv = - 2 Ω dr

Fig. 5.11
Comme le montre la figure 5.11
dr = dy sin Lat
soit
dv = - 2 Ω dy sin Lat
On peut maintenant calculer l'accélération dv/dt correspondante,
c'est-à-dire la force par unité de masse:
dv/dt = - 2 Ω dy/dt sin Lat
d'où enfin
C = - 2 Ω v sin
Lat
où v est la vitesse de déplacement de la masse unité sur l'axe
nord-sud. Dans le cas de la figure 5.11, v est négatif (comme
dLat) car la masse de
déplace vers le sud, d'où C positif.
On peut de la même manière calculer la force de Coriolis liée à un
déplacement vers le zénith du lieu, mais cela n'a guère d'utilité en
météorologie où les déplacements verticaux se font à vitesse très
faible.
Dans le cas général d'un mouvement 'horizontal' (c'est-à-dire
sans composante verticale) à la surface de la
terre, il suffit de décomposer le vecteur vitesse en ses deux
composantes selon l'axe est-ouest et l'axe nord-sud.
Note 1
Comme la force centrifuge, la force de Coriolis est une pseudo-force
dans la mesure où elle n'apparaît que lorsque nous considérons la terre
comme un référentiel galiléen (ou inertiel) en mouvement de translation
rectiligne uniforme (éventuellement au repos, à vitesse nulle) et non
comme un référentiel en rotation, comme c'est le cas en réalité.
C'est pourquoi certains auteurs préfèrent le terme d'effet Coriolis,
évitant le terme 'force' ou 'accélération' (à l'origine d'une force).
Il n'y pas d'inconvénient à traiter cette pseudo-force comme une force
dans les raisonnements et les calculs, à condition de se souvenir que
la notion de travail n'a aucun sens dans le cas des pseudo-forces.
Note 2
De manière plus précise, la vitesse angulaire a pour unité s-1.
Voici pourquoi.
La mesure d'un angle est définie par le rapport entre une longueur
mesurée sur la circonférence et le rayon. Par exemple, une longueur
unité mesurée sur un cercle de rayon unité correspond à un angle de 1
radian. Un angle, étant le rapport entre deux longueurs, est un nombre
pur, sans dimensions, donc sans unité. Le radian n'est donc qu'une
pseudo-unité, à la valeur simplement pratique. La vitesse angulaire,
exprimée en radians par seconde, est donc strictement le rapport d'un
nombre par un temps: il a donc comme unité s-1
Note 3
Selon Newton, la force gravitationnelle Fg
exercée par un élément de masse M sur un élément de masse m séparés
d'une distance r = |r|
est donnée par
Fg
=
- (G M m / r²) (r
/ r)
où G est la constante gravitationnelle (6,6742×10-11
N m2 kg−2)
r est la distance entre les centres des
masses
r
/ r est le vecteur unité dirigé de M
vers m
Le signe moins résulte du fait que nous voulons la force
gravitationnelle de M sur m.

En météorologie, la distance entre les masses d'air concernées et la
surface
du globe (ordre de grandeur 5 km) est négligeable par rapport au rayon
terrestre (6370 km) dans le calcul de g.
Notons à nouveau que si la terre était parfaitement
sphérique, la force
centrifuge induirait une composante méridienne (vers l'Equateur) (voir
fig. 2.3). Ce n'est pas le cas en raison de la forme ellipsoïdale qu'a
adoptée la terre au cours de son histoire (fig. 2.1)
 Retour à la page d'accueil
Retour à la page d'accueil
Version 1.0 le 23/10/ 2012 à
09h:55


































 Retour à la page d'accueil
Retour à la page d'accueil