10 - La formule
fondamentale de la navigation astronomique
 Retour à la page d'accueil
Retour à la page d'accueil
Muni de la 'loi des cosinus', nous
sommes maintenant prêts à démontrer cette formule. Nous le ferons dans un premier temps sans
référence à la signification concrète des points, des distances et des
angles.
Cela viendra ensuite...
PS J'ai mis au point cette démonstration contournant l'emploi de
théorèmes de la géométrie dite sphérique il y a bien longtemps et sans
l'aide de sources. Elle est peut-être originale, mais je ne peux
l'assurer...

Fig.1
Considérons
deux
segments de droites OA et OB d'orientation
quelconque dans
l'espace, de même origine O, et de
longueur a et b dans un
repère tridimensionnel xyz orthonormé (les 3
axes sont perpendiculaires entre eux, avec la même unité de
mesure sur chacun). (Fig. 1)
Soit
A' la projection (perpendiculaire) de A sur le plan xOy et B' la
projection de B sur ce
même plan (= toutes les droites du plan xOy passant par A'
seront
perpendiculaires à AA', de même celle passant par B' par
rapport à
BB')
Traçons A'O et B'O
On suppose que l'on connaît
α
(l'angle
A'OA)
β
(l'angle B'OB) et
δ (l'angle
B'OA').
On
veut calculer γ, l'angle AOB.
Pour ce faire, nous allons calculer la longueur du segment AB de deux manières différentes.
On
a OA'
= a cos α
OB'
= b cos β
On
peut calculer A'B'² en
utilisant la loi des cosinus
A'B'² = OA'² + OB'² - 2 OA'
OB' cos δ = a² cos² α
+ b² cos² β
- 2 a b cos α
cos β cos δ
On
a également
AA' = a sin α
BB'
= b sin β
Comme
les droites AA' et BB' sont toutes deux perpendiculaires au plan xOy,
elles sont parallèles entre elles, donc perpendiculaires à
A'B' qui est une droite de ce plan passant par A' et B'.
Traçons
B"A parallèle à B'A' pour former le rectangle AA'B'B". Le quadrilatère
AA'B'B est donc composé du
rectangle AA'B'B" surmonté du triangle rectangle AB"B.
Dans
le triangle rectangle AB"B, AB"² = A'B'² = a² cos² α
+ b² cos² β
- 2 a b cos α
cos β cos δ
Comme AA' = B"B' = a sin α,
on
a BB" = BB' - A'A" = b sin β
- a sin α
On
peut
maintenant calculer AB par le théorème de Pythagore :
AB² =
BB"² + AB"²
= (b sin β
- a sin α)²
+ a² cos² α
+ b² cos² β
- 2 a b cos α
cos β cos δ
= b² sin² β
-
2 a b sin α sin β
+ a²
sin² α + a²
cos² α
+ b² cos² β
- 2 a b cos α
cos β cos δ
= a² (sin² α +
cos² α) +
b² (sin² β +
cos² β) -
2 a b sin α
sin β - 2
a b cos α
cos β cos δ
Comme
sin² α +
cos² α =
sin² β +
cos² β = 1
AB²
= a² + b² -
2 a b ( sin α
sin β +
cos α
cos β cos δ)
Considérons maintenant le triangle OAB. En
utilisant à nouveau la loi des cosinus, la longueur du segment AB est donnée par
AB²
= a² + b² - 2 a b cos γ
On
obtient ainsi l'égalité AB²
= a² + b² - 2 a b cos γ
= a² + b² - 2 a b ( sin α
sin β +
cos α
cos β cos δ)
Cette
égalité est vraie si
cos γ = sin α sin β + cos α cos β cos δ
Le
but est atteint: on sait maintenant calculer γ en
fonction de α
, β et δ
On
remarque que cette
relation est indépendante du choix des longueurs a
et b: elle ne fait appel qu'à la valeur des 4
angles.
L'emploi
de la formule fondamentale de la navigation astronomique
Il
est temps de passer à l'emploi de la formule fondamentale dans le
calcul du point. Les éléments pertinents sont sur la fig. 5

Fig. 5
L'observateur
est au point A. Ce point est repéré par une latitude
(l'angle α) , par exemple 46° N, et une longitude, par exemple
12° W.
L'axe prolongeant OA est celui du zénith du lieu,
plus familièrement l'axe de la verticale du point A.
L'axe prolongeant OB est la
direction du soleil à partir du centre de la Terre. Cet axe coupe la
surface de la Terre en un point qu'on appelle parfois de manière imagée
le "pied du soleil". A cet endroit sur Terre, le soleil est à la
verticale (= au zénith) du lieu.
La projection de l'axe du zénith du
lieu et
celle de la direction du soleil sur l'équateur (ici OL et
OS)
font un angle δ sur le plan de
l'équateur, appelée angle
horaire, parce qu'il varie en
fonction de l'heure de la journée en raison de la rotation de la terre.
Pour
chaque instant d'une journée, des tables (les éphémérides
nautiques, 'nautical almanach' en anglais) nous permettent de connaître
- la déclinaison
du soleil (l'angle β, l'équivalent de sa latitude) et
- l'angle horaire.
Ce que fait la formule fondamentale de la
navigation astronomique, c'est de permettre le calcul de l'angle γ entre la
direction du soleil et l'axe du zénith du lieu.
La
connaissance de cet angle est indispensable pour faire le point.
Une dernière (petite) difficulté:
Le sextant
mesure
l'angle h entre la direction du soleil et celle de l'horizon, appelée la
hauteur du soleil, et pas l'angle entre la direction du soleil et la verticale du lieu.
Cette difficulté n'est pas compliquée à
résoudre: la direction du zénith étant perpendiculaire
à celle de l'horizon, on h = 90° - γ (fig.5)

Fig. 5
Or sin h = sin
(90° - γ) (= sin (π/2 - γ)) =
cos γ
// sin (π/2 - γ) = sin π/2
cos γ -
cos π/2 sin γ = cos γ
car sin π/2 = 1
et cos π/2 = 0
La formule fondamentale de la navigation astronomique peut s'écrire
sin h
= cos Lat cos Dec cos AH + sin
Lat sin Dec
où
h
est la hauteur du soleil, l'angle entre la direction du soleil et l'horizon.
C'est cette formule qui est à la base de toutes les méthodes et tables permettant la navigation astronomique...
Il ne reste plus qu'à savoir comment s'y prendre de manière concrète.
Mais cela, c'est l'affaire, comme nous l'avons déjà, d'un excellent
site comme http://navastro.free.fr
Distance
(orthodromique) entre deux points
Appliquée
à la Terre considérée comme une sphère, la formule fondamentale de la
navigation astronomique va
immédiatement nous permettre de calculer la distance sur la surface
entre deux points sur la Terre (distance
dite orthodromique).
Prenons un exemple concret :
Soit deux lieux A et B à la
surface du
globe.
Les coordonnées géographiques de A sont : latitude
51° N, longitude 12° E.
Les coordonnées géographiques
de B sont : latitude 15° N, longitude 55° W.
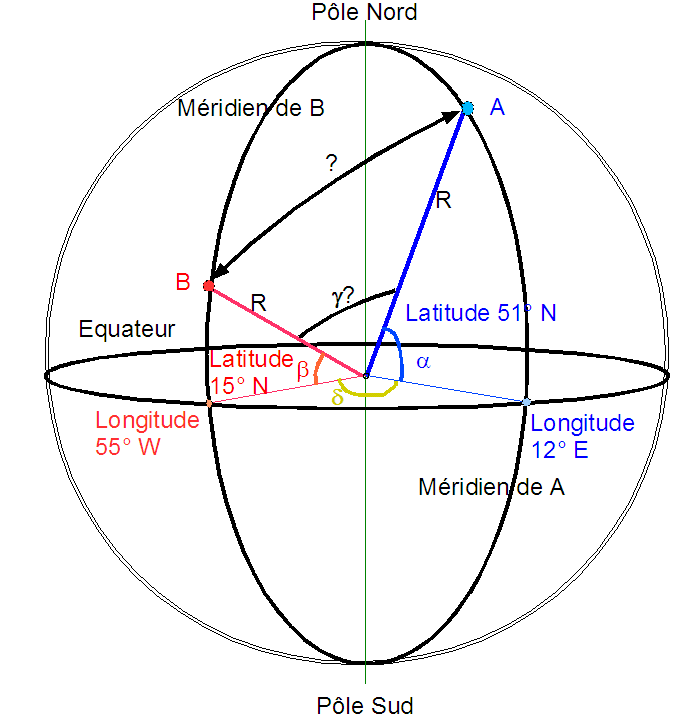
Fig. 4
α est
la
latitude du point A (LatA = 51° N) , β est la latitude du point B (LatB
= 15° N), δ est l'écart entre
les longitudes de A et B (12 + 55 = 67°), et γ est l'angle au centre
des directions des points A et B
Selon cette fameuse formule
cos
γ = sin LatA sin LatB + cos LatA cos LatB cos δ
La
distance
entre A et B est un arc de cercle de rayon R situé aux extrémités des
deux
rayons OA et OB qui font un angle γ entre eux.
Numériquement
cos γ = sin 51°
sin 15° + cos 51° cos 15° cos 67°=
0,4386566...
d'où γ = 63,98° Si
on remarque que 1
minute d'angle (1') sur
la surface de la Terre correspond à 1 mille
marin (1 M) (ou mille nautique par
anglicisme fréquent de
'nautical mile'), on voit qu'il suffit de transformer la valeur de γ
en minutes
pour trouver
la
distance en milles marins (un ° vaut bien sûr
60'). γ vaut 63,98*60
= 3839'
, donc la distance entre A et B est de 3839 M
NB
: 3844 M selon le système géodésique
WGS84 voir http://williams.best.vwh.net/gccalc.htm)
On
remarque que la valeur du rayon de la Terre R ne joue aucun rôle !
C'est la magie de l'utilisation du mille marin, qui est en fait une
valeur d'angle !
On peut bien sûr calculer cette
distance en utilisant la valeur du rayon. La longueur de l'arc de
cercle AB est R γ,
si γ est
exprimé en radians !
γ vaut 1,11669.. radians. Le
rayon de la Terre vaut environ 6370 km, d'où une distance de R
γ
= 7122 km,
c'est-à-dire 3840 M.
Profitons
en pour calculer la valeur en km du mille marin. La circonférence de la
Terre fait (à peu de chose près) 40 000 km, ce qui correspond à 360
x 60' = 21600'. Donc 1' correspond à 40 000 km / 21600 = 1,852 km (cf
http://fr.wikipedia.org/wiki/Mille_marin)
WGS84
Equatorial
radius 6378,1370 km
Polar radius
6356,7523142 km
Flattening 1/298.25722
NB:
Dans l'exemple
ci-dessus, les latitudes étaient N. Si les latitudes sont S,
il
faut
La formule fondamentale de la
trigonométrie sphérique, pour la culture....
Cette
partie n'est certainement pas indispensable. Mais au point où nous en
sommes, il est facile de démontrer la formule fondamentale de la
trigonométrie sphérique, pour la culture et pour voir le rapport étroit
entre
la formule utilisée pour la navigation astronomique et le la
formule fondamentale de la trigonométrie sphérique.
Soit
une sphère de rayon R (Fig. 2) Traçons OA et OB, cette fois comme deux
rayons quelconques de la sphère. Les
angles α
et β
sont les angles entre les rayons OA et OB et le plan perpendiculaire au
rayon OC passant par le centre de la sphère O (qui équivaut au plan xOy
de la demonstration précédente : si C est vu comme le
pôle Nord, ce plan contient l'équateur, et α et β sont les
latitudes des points
A et B. Considérons
le triangle dit sphérique CAB sur cette sphère.
La
longueur du côté b (= la portion de l'arc de cercle entre C et
A) a pour valeur R(π/2
-
α) (la valeur (en
radians) de l'angle π/2 -
α, c'est-à-dire l'angle entre les rayons OC et OA, multiplié par la
mesure R du rayon).
De même, la longueur du côté a,
entre C et B, a pour
valeur R(π/2 - β),
la valeur de l'angle entre les rayons
OC et OB multiplié par R.
Enfin, la longueur du côté c, entre
B et A, a pour valeur
R γ
En un mot
b = R(π/2
- α)
a = R(π/2 - β)
c = R γ
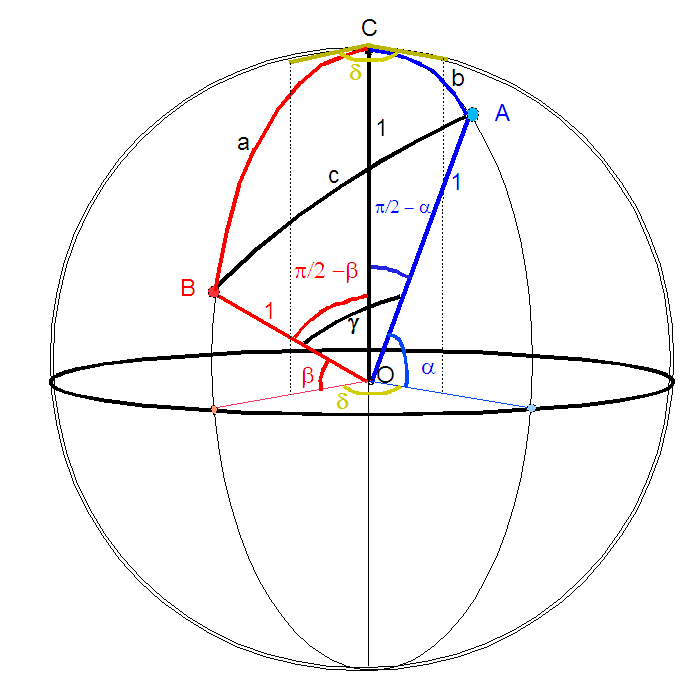
Fig. 2
On
définit l'angle
C entre les côtés a et b de la
manière
suivante : on trace en
C les tangentes aux côtés a et b. Ces tangentes sont dans un plan qui
contient le pôle C. L'axe du pôle est perpendiculaire à ce plan (sinon
ce plan couperait une partie de la sphère !). Il est donc parallèle au
plan "équatorial" (= le plan
lui aussi perpendiculaire à OC passant par O). Ces tangentes
sont donc elles aussi parallèles au plan "équatorial".
L'angle C est défini comme
l'angle entre ces deux tangentes. C'est l'angle entre les deux
demi-plans
(coupant la sphère en quart de cercle) qui contiennent CBO pour l'un et
CAO pour l'autre
(les plans "méridiens" de B et C). Cet angle n'est autre que δ. Donc
C
= δ (Ouf...)
Reprenons la
formule démontrée plus haut : cos γ = sin α sin β + cos α cos β cos δ
On a
b
= R(π/2
- α) c'est-à-dire b/R = π/2
- α
a = R(π/2 - β) c'est-à-dire a/R = π/2
- β
c = R γ c'est-à-dire
c/R = γ
Or
sin a/R = sin (π/2
- β) = cos β
// sin
(π/2 - β) =
sin π/2 cos β - cos π/2 sin β = cos β car
sin π/2 = 1 et cos π/2 = 0
sin b/R = sin (π/2
- α) = cos α
cos
a/R = cos
(π/2
- β) = sin β
// cos
(π/2 - β) = cos π/2 cos β + sin π/2 sin β = sin β
car sin π/2 = 1 et cos π/2 = 0
cos b/R = cos (π/2
- α) = sin α
cos c/R = cos γ
C
= δ
d'où,
en reportant
dans la formule
cos c/R = cos b/R
cos a/R
+ sin b/R sin a/R
cos C
On écrit généralement
cette formule pour un rayon unité (R = 1) d'où
cos
c = cos b
cos a
+ sin b sin a
cos C

Fig. 3
En toutes lettres :
Sur
une sphère de rayon unité, la longueur du côté c (qui n'est
pas
autre chose que la valeur d'un angle !) peut être calculée à
partir de
la longueur des côtés a et b et de la valeur de l'angle C, à
l'opposé de c.
Ou alors, sur une sphère de rayon R, la longueur
c/R (également la valeur d'un angle !) peut être calculée à
partir des longueur a/R et b/R et de la valeur de l'angle C, à l'opposé
de c.
On
peut ainsi calculer la distance entre deux points A et B si l'on
connait les distances AC et CB à un troisième point C et l'angle entre
la direction de A et celle de B en ce point C. Ce cas n'est pas très
fréquent en pratique !
Le plus souvent on cherche la
distance
entre A et B connaissant les coordonnées géographiques de A et B, et
c'est ce nous a permis la formule fondamentale de la
navigation astronomique !
cos
c = cos b
cos a
+ sin b sin a
cos C
sin b sin a cos C = cos c - cos b cos
a
cos C = (1 / sin b) (1 / sin a) = (cos c - cos b
cos a)
Or 1 / sin α est appelée la cosécante de α
(cosec α), d'où la formule
cos C = cosec b cosec a
(cos c - cos b
cos a)
ou alors, cos α / sin α étant
la cotangente de α (cotg α)
cos C = cos
c / (sin b sin a) - cotg b cotg a
Pour
permettre le calcul logarithmique, on peut dériver les formules
suivantes
cos C = cos (C/2 + C/2) = cos C/2 cos C/2 - sin C/2
sin C/2 = cos² C/2 - sin² C/2.
Comme cos² C/2 + sin² C/2 = 1 ,
cos² C/2 = 1 - sin² C/2 d'où
cos C = 1 - 2 sin² C/2
La
formule fondamentale s'écrit
cos
c = cos b
cos a
+ sin b sin a
cos C
cos
c = cos b
cos a
+ sin b sin a
cos C = cos
b
cos a
+ sin b sin a (1 - 2 sin² C/2) = cos b
cos a
+ sin b sin a - 2 sin b sin a sin² C/2
Comme cos b
cos a
+ sin b sin a = cos (b - a)
cos c = cos (b - a) - 2 sin b sin
a sin² C/2
cos (b - a) - cos c = 2 sin b sin a sin² C/2
De
plus
Soit p = α + β et q = α
- β
p + q = 2α
p - q = 2β
cos (α - β) -
cos (α + β) = cos q - cos p = cos α cos β + sin α sin β - cos
α cos β + sin α sin β = 2 sin α sin β = 2
sin ((p + q) / 2) sin ((p - q) / 2)
cos q - cos p = 2 sin ((p
+ q) / 2) sin ((p - q) / 2).
On peut donc écrire, avec q = b -
a et p = c
cos (b - c) - cos c = 2 sin (c /
2 + (b - a) / 2) sin (c / 2 - (b + c) / 2)
d'où
2
sin (c + (b - a) / 2) sin (c - (b - a) / 2) = 2 sin
b sin a sin² C/2
Définissons 2s = a + b + c d'où
c +
(b - a) = c + b - a = a + b + c - 2 a = 2 s - 2 a = 2 (s - a)
c -
(b - a) = c - b + a = a + b + c - 2 b = 2 s - 2 b = 2 (s - b)
On
tire
2 sin (s - a) sin (s - b) = 2 sin b sin a sin² C/2
d'où
sin²
C/2 = sin (s - a) sin (s - b) / sin b sin a
et
sin
C/2 = √ (sin (s - a) sin (s - b) / sin b sin a)
[avec s = (a + b + c) / 2)]
 Retour à la page d'accueil
Retour à la page d'accueil
 Retour à la page d'accueil
Retour à la page d'accueil





 Retour à la page d'accueil
Retour à la page d'accueil